Solve and Graph inequalities and Absolute Value

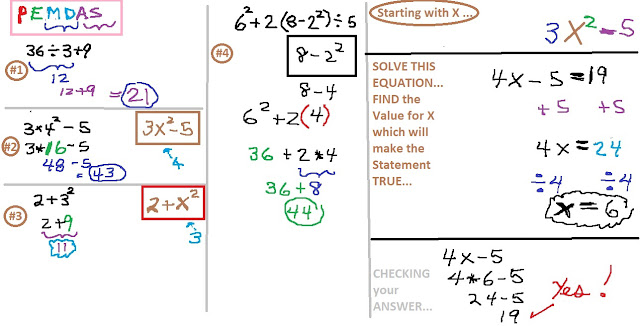
REVISITING the PEMDAS

You may want to print the jpg below
before you watch the video...

This Video show how to UNDO the process
so we can ISOLATE the X
to SOLVE an EQUATION

******************************************* 

Understanding the INEQUALITY

 Graphing an Open Sentence

that is an INEQUALITY.

(Marking all NUMBERS that will
MAKE the INEQUALITY TRUE.)

For example:

Graph the Solution Set for   "5 <  x"

" the >  or < will NOT ALWAYS point in the

direction of the shaded solution. 

SINCE  "5 < x" is EQUIVALENT TO "x > 5"

the graph is  ...

By READing the inequality starting with "X".

"5 < x"

would be read "X is GREATER than 5."

Since we are graphing "X's", this method

of translation will lead to the correct

direction of the ARROW in the graph.

OR TESTING A FEW NUMBES 
Back into the ORIGINAL PROBLEM
to be sure that they MAKE IT TRUE

*********************************************************

******************************************************

********************************************************

As can be seen in the above video,

some problems have MORE THAN ONE CORRECT SOLUTION

**********************************************************

.If you Click on an image

a LARGER view will appear.

A general discussion of 

No SOLUTION vs. All REAL NUMBERS 

(This has similar results with = EQUATIONS)

Here is a More Difficult Inequality 

where the VARIABLES completely disappear

 when we try to get them onto one side of < or > or even =

**************STOP HERE***************

The problems below are MORE DIFFICULT.

Your class may never do this level of problem.

Square Root Symbol, Absolute Value Symbol, etc

Square Root Symbol, Absolute Value Symbol, etc